EL TEOREMA
DE BOUCHEROT
Ideado por Paul
Boucherot, permite la resolución del cálculo total de potencias en circuitos de corriente alterna. De acuerdo con este
teorema, las potencias
activa y reactiva totales en un circuito,
vienen dadas por la suma de las potencias activa y reactiva, respectivamente,
de cada una de sus cargas. De forma analítica.
RECEPTOR EN SERIE:
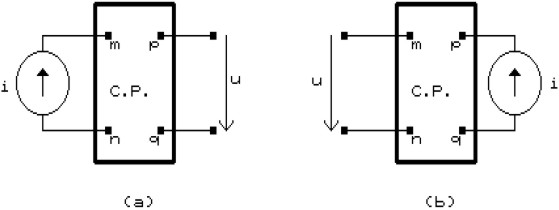
Sea el circuito serie de la figura 1a. Aplicando la ley de Ohm
Tomando la intensidad en el origen de fases (figura 1b),
sustituyendo:
RECEPTOR EN SERIE.
Sea el circuito paralelo y su correspondiente diagrama fasorial, figuras 2a y 2b respectivamente. Las componentes activa y reactiva de la corriente total, 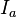 e
e  , vienen dadas como suma de las componentes parciales de cada una de la corrientes que circulan por cada rama:
, vienen dadas como suma de las componentes parciales de cada una de la corrientes que circulan por cada rama:
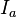 e
e  , vienen dadas como suma de las componentes parciales de cada una de la corrientes que circulan por cada rama:
, vienen dadas como suma de las componentes parciales de cada una de la corrientes que circulan por cada rama:
Sustituyendo por sus valores:
Y si estas expresiones se multiplican por V, se obtiene
Que es el mismo resultado que para un receptor serie. En ambos casos, generalizando
que es lo que se deseaba demostrar.
EL TEOREMA DE FORTESCUE
Conocido como el teorema de las componentes simétricas es uno
de los teoremas más importantes en la ingeniería eléctrica. Se
utiliza para simplificar el análisis de los sistemas de energía trifásicos
desequilibrados, pues permite escribir de forma general un sistema polifásico desbalanceado
(con n fases) como la suma de n sistemas equilibrados aplicando el principio de
superposición. Siempre y cuando las corrientes y tensiones del
sistema se relacionen con impedancias lineales de otro modo el principio de
superposición no es aplicable.
El teorema
fue presentado por primera vez por Charles Legeyt Fortescue en un
artículo presentado en 1918 intitulado "Method of Symmetrical Co-Ordinates Applied to the Solution of Polyphase
Networks". El artículo fue adoptado en empresas del sector
eléctrico usándose en el ajuste del sistema de protecciones y
dimensionamiento de equipos.
Expandiendo
un diagrama de una línea para mostrar la
secuencia positiva, secuencia negativa e impedancias de secuencia cero de
generadores y transformadores y otros dispositivos, en el análisis las
condiciones de desbalanceo de la línea sencilla a tierra por una falla o fuga
de corriente de corto
circuito se simplifica considerablemente. La técnica también
puede extenderse su uso para sistemas con mayor cantidad de fases.
Físicamente,
en un sistema trifásico, un
conjunto de corrientes positivas producen un campo rotatorio
normal, un conjunto de secuencias negativas producen un campo con rotación
opuesta y la secuencia cero produce un campo que oscila pero no gira. Desde que
estos efectos pueden ser detectados físicamente, la herramienta matemática
llegó a ser la base para el diseño de relevadores de
protección, los cuales usan voltaje y corrientes
de secuencia negativa como un indicador confiable de condiciones de falla.
Dichos relevadores deben ser usados para activar los disyuntores (en
inglés, "breakers") o interruptores automáticos o seguir otros pasos
para proteger sistemas eléctricos. La técnica analítica fue adoptada y mejorada
por ingenieros de General Electric y Westinghouse y
después de la Segunda Guerra Mundial, el método fue aceptado para el análisis
de de sistemas asimétricos.
EL TEOREMA DE KENNELLY
Llamado así en homenaje a Arthur Edwin Kennelly, permite determinar la carga equivalente en estrella a una dada en triángulo y viceversa. El teorema también se le suele llamar de transformación estrella-triángulo (escrito Y-Δ) o transformación te-delta (escrito T-Δ).
ECUACIONES DE TRANSFORMACIÓN
En la siguiente tabla se muestran las ecuaciones de transformación en función de las impedancias y de las admitancias.
| Ecuaciones de Kennelly | ||||||||
|---|---|---|---|---|---|---|---|---|
| Transformación Δ-Y | ||||||||
| ||||||||
| Transformación Y-Δ | ||||||||
|
EL TEOREMA DE NORTÓN
Es dual del teorema de Thévenin. Se conoce así en honor al ingeniero Edward Lawry Norton, de los Laboratorios Bell, que lo publicó en un informe interno en el año 1926. El alemán Hans Ferdinand Mayer llegó a la misma conclusión de forma simultánea e independiente.
Establece que cualquier circuito lineal se puede sustituir por una fuente equivalente de intensidad en paralelo con una impedancia equivalente.
Al sustituir un generador de corriente por uno de tensión, el borne positivo del generador de tensión deberá coincidir con el borne positivo del generador de corriente y viceversa.
CÁLCULO DEL CIRCUITO NORTON EQUIVALENTE
El circuito Norton equivalente consiste en una fuente de corriente INo en paralelo con una resistencia RNo. Para calcularlo:
- Se calcula la corriente de salida, IAB, cuando se cortocircuita la salida, es decir, cuando se pone una carga (tensión) nula entre A y B. Al colocar un cortocircuito entre A y B toda la intensidad INo circula por la rama AB, por lo que ahora IAB es igual a INo.
- Se calcula la tensión de salida, VAB, cuando no se conecta ninguna carga externa, es decir, cuando se pone una resistencia infinita entre A y B. RNo es ahora igual a VAB dividido entre INo porque toda la intensidad INo ahora circula a través de RNo y las tensiones de ambas ramas tienen que coincidir ( VAB = INoRNo ).
TEOREMA DE RECIPROCIDAD
Es un teorema muy usado en análisis de circuitos. El teorema de reciprocidad cuenta con dos enunciados que en términos generales nos dice:
En cualquier red bilateral real pasiva, si la fuente de tensión simple Vx en la rama x produce la respuesta en corriente Iy en la rama y, entonces la eliminación de la fuente de tensión en la rama x y su inserción en la rama y produciría la respuesta en corriente Iy
PRIMER ENUNCIADO:
Indica que si la excitación en la entrada de un circuito produce una corriente i a la salida, la misma excitación aplicada en la salida producirá la misma corriente i a la entrada del mismo circuito. Es decir el resultado es el mismo si se intercambia la excitación y la respuesta en un circuito. Así:
SEGUNDO ENUNCIADO:
La intensidad i que circula por una rama de un circuito lineal y pasivo, cuando se intercala una fuente de tensión en otra rama, es la misma que circularía por esta última si la fuente de tensión se intercalase en la primera.
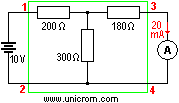
EJEMPLO SIMPLE:
En el siguiente circuito se tiene una fuente de tensión en corriente directa de 10 Voltios, entre 1 y 2, que alimenta una red de resistencias.
Si ahora se cambian de posición la fuente de tensión y el amperímetro, quedando la fuente de tensión entre 3 y 4, y el amperímetro entre 1 y 2, como se muestra en el siguiente diagrama:
Se observa que en el amperímetro se lee una corriente de 20 mA. En conclusión se puede afirmar que: "El hecho de intercambiar la posición relativa de los puntos de inserción de la fuente y del amperímetro no modifica los valores medidos".
LEY DE OHM
Postulada por el físico y matemático alemán Georg Simon Ohm, es una ley de la electricidad. Establece que la diferencia de potencial  que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente
que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente  que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica
que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica  ; que es el factor de proporcionalidad que aparece en la relación entre
; que es el factor de proporcionalidad que aparece en la relación entre  e
e  :
:
 que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente
que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente  que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica
que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica  ; que es el factor de proporcionalidad que aparece en la relación entre
; que es el factor de proporcionalidad que aparece en la relación entre  e
e  :
:
La fórmula anterior se conoce como ley de Ohm incluso cuando la resistencia varía con la corriente, y en la misma,  corresponde a la diferencia de potencial,
corresponde a la diferencia de potencial,  a la resistencia e
a la resistencia e  a la intensidad de la corriente. Las unidades de esas tres magnitudes en el sistema internacional de unidades son, respectivamente, voltios (V), ohmios (Ω) y amperios (A).
a la intensidad de la corriente. Las unidades de esas tres magnitudes en el sistema internacional de unidades son, respectivamente, voltios (V), ohmios (Ω) y amperios (A).
 corresponde a la diferencia de potencial,
corresponde a la diferencia de potencial,  a la resistencia e
a la resistencia e  a la intensidad de la corriente. Las unidades de esas tres magnitudes en el sistema internacional de unidades son, respectivamente, voltios (V), ohmios (Ω) y amperios (A).
a la intensidad de la corriente. Las unidades de esas tres magnitudes en el sistema internacional de unidades son, respectivamente, voltios (V), ohmios (Ω) y amperios (A).
Otras expresiones alternativas, que se obtienen a partir de la ecuación anterior, son:
 válida si 'R' no es nulo
válida si 'R' no es nulo
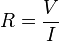 válida si 'I' no es nula
válida si 'I' no es nula
En los circuitos de alterna senoidal, a partir del concepto de impedancia, se ha generalizado esta ley, dando lugar a la llamada ley de Ohm para circuitos recorridos por corriente alterna, que indica:
Donde  corresponde al fasor corriente,
corresponde al fasor corriente,  al fasor tensión y
al fasor tensión y  a la impedancia.
a la impedancia.
 corresponde al fasor corriente,
corresponde al fasor corriente,  al fasor tensión y
al fasor tensión y  a la impedancia.
a la impedancia.
LAS LEYES DE KIRCHHOFF
Son dos igualdades que se basan en la conservación de la energía y la carga en los circuitos eléctricos. Fueron descritas por primera vez en 1845 por Gustav Kirchhoff. Son ampliamente usadas en ingeniería eléctrica.
Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado. Estas leyes son muy utilizadas en ingeniería eléctrica e ingeniería electrónica para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico.
LEY DE CORRIENTE DE KIRCHHOFF
Esta ley también es llamada ley de nodos o primera ley de Kirchhoff y es común que se use la sigla LCK para referirse a esta ley. La ley de corrientes de Kirchhoff nos dice que:
|
Esta fórmula es válida también para circuitos complejos:
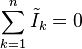
La ley se basa en el principio de la conservación de la carga donde la carga en couloumbs es el producto de la corriente en amperios y el tiempo en segundos.






























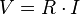
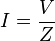


No hay comentarios.:
Publicar un comentario